Home - SCIENCE WAVE
사이언스 웨이브(Science Wave)는 세상을 과학의 눈으로 바라봅니다. 최신 과학뉴스와 누구나 쉽고 재미있게 볼 수 있는 과학상식을 전달합니다.
sciencewave.kr
그래서 아까 가정했던 낙하운동의 속력이 낙하시간에 비례하는 경우를 생각해 보자. 그때 속력, 즉 속도의 크기가 변화하기 때문에 가속도가 있다. 그러나 속도의 방향은 늘 연직선 위를 아래로 향해 있어서 변화하지 않기 때문에 속도의 변화, 따라서 가속도의 방향도 늘 연직 방향 아래로 향해 있다는 것이 분명하다.
그런데 어떤 낙하시간 내에, 속력이 얼마만큼 변화하느냐 하면, 그것은 최종 속력으로부터 처음 속력을 빼면 된다. 그러나 처음 정지 상태로부터 낙하를 시작한 경우를 고찰하고 있으므로, 최종 속력, 즉 속력의 변화 자체이기도 하다. 그리고 속력 이 낙하시간에 비례하여 증대한다면 속력의 변화도 또 낙하시간에 비례해서 증대하게 된다. 즉 낙하시간이 2배가 되면 속력의 변화도 2배가, 시간이 3배가 되면 변화도 3배가 된다. 따라서 속력의 변화를 낙하시간으로 나눈 것, 즉 가속도의 크기는 낙하시간을 어떻게 잡든지 간에 늘 같은 값을 갖고 있다는 것을 안다.
따라서 우리의 가정은 다음과 같이 고쳐 쓸 수 있다. 「낙하운동의 가속도 크기는 늘 일정하며, 임의의 낙하시간 후의 속력을 그 낙하시간으로 나눈 것과 같다.」 즉 물체가 어떤 시간(t)만큼 낙하했을 때의 속력을 v라고 하면, 낙하운동의 가속도 크기(g)는 다음과 같이 주어진다.
g = v/t : 일정 …………… <수식 1-1>
따라서
v = gt …………… <수식 1-2>
즉 「낙하운동의 속도는 가속도의 크기(일정)에 낙하시간을 곱한 것과 같다」고 된다. <수식 1-2>는 <수식 1-1>의 비례상수를 g로 둔 것이다.
또 낙하운동에서는 가속도의 크기, 방향이 모두 일정하므로 우리의 가정은 「낙하운동은 등가속도 운동이다」라고 표현해도 된다.
낙하운동의 법칙
그런데 우리의 가정은 이상의 고찰로서도 분명하듯이 이론적인 모순을 내포하고 있다고 생각되지 않는다. 그래서 실험에 의해 이 가정을 확인하게 되는데, 다만 그때 속력을 측정하는 것은 어렵기 때문에 속력과 시간의 관계를 주고 있는 이 가정으로부터 다시 거리와 시간의 관계를 유도하여 그것을 실험과 비교해 보자.

지금 가로축에 운동시간, 세로축에 속도를 잡고, 여러 가지 운동의 그래프, 즉 속력 곡선을 그려보자.
우선 등속운동일 경우 그래프는 가로축에 평행한 직선이 된다(그림 4). 잘 알려져 있듯이 등속도 운동에서 운동거리(s)는 속력(v)에 운동시간(t)을 곱한 것과 같다. 즉
s = vt …………… <수식 1-3>
이다. 그리고 이것은 마침, 직선 밑에 둘러싸인 직사각형의 면적 바로 그것이다.

일반적으로 속력이 시간과 더불어 변하는 경우에 그래프는 하나의 곡선을 그린다. 그래서 운동시간을 많은 짧은 시간대로 쪼개고, 각각의 짧은 시간 내에는 등속도 운동을 한다고 본다면, 속력 곡선은 계단 모양이 되고, 운동거리는 계단 밑의 각 직사각형의 면적의 합과 같아진다. 운동시간의 분할 방법을 무한히 세밀하게 하면 그 극한으로서 계단은 본래의 곡선과 일치하고, 운동거리는 곡선 밑에 둘러싸인 면적과 같아질 것이다(그림 5).

특히 우리의 가정, 속력이 운동시간에 비례하고 있을 경우에 그래프는 원점을 통과하는 직선이 된다. 따라서 그 운동거리는 이 직선 밑에 둘러싸인 삼각형의 면적과 같고, 최종 속력과 운동시간을 곱한 것의 절반으로 주어진다(그림 6).
이렇게 하여 「낙하운동의 속도는 낙하시간에 비례한다」고 가정하면 「낙하거리는 속도와 낙하시간을 곱한 것의 절반과 같다」는 것을 안다. 즉 낙하거리를 s, 속력을 v, 낙하시간을 t로 하면,

이다. 그런데 속력과 낙하시간의 관계는 이미 <수식 1-2>로 주어져 있으므로, 이것을 <수식 1-4>에 대입하면, 낙하거리는
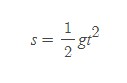
으로 나타낼 수 있다. 여기서 s는 낙하거리, t는 낙하시간, g는 낙하운동의 가속도 크기다.
즉 「낙하거리는 낙하시간의 제곱에 비례한다」가 된다. 낙하시간이 2배가 되면 낙하거리는 4배로, 시간이 3배가 되면 거리는 9배가 되는 셈이다.
이것이 실험과 비교돼야 할 낙하거리와 낙하시간의 관계다.
그리고 실험에 따르면 <수식 1-5>가 옳다는 것, 따라서 우리의 가정이 옳다는 것이 확인된다. 이렇게 하여 우리는 갈릴레오의 낙하운동의 법칙에 도달할 수 있었다.
또한 실험에 따르면, 낙하운동의 가속도 크기는,

g = 980㎝/s2 = 9.8m/s2 …………… <수식 1-6>
로써 주어진다.
가속도는 속도의 시간과 더불어 변하는 정도이기 때문에, 그 단위는 속도의 단위를 시간의 단위로 나눈 것, 즉 길이의 단위를 시간의 단위의 제곱으로 나눈 것이 된다.
또 하나의 길도 있었다
그런데 낙하운동 속도의 낙하시간에 대한 관계는 <수식 1- 2>에서 주어지고, 낙하거리의 낙하시간에 대한 관계는 <수식 1-5>로 주어졌다. 그래서 <수식 1-2>와 <수식 1-5>로부터 시간(t)을 소거하면, 낙하운동의 속력(v)의 낙하거리(s)에 대한 관계가 구해진다.
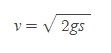
즉, 「낙하운동의 속력은 낙하시간에 비례한다」, 「낙하거리는 낙하시간의 제곱에 비례한다」는 것으로부터 「낙하운동의 속력은 낙하거리의 제곱근에 비례한다」는 것이 이끌어졌다.
우리는 아까 낙하운동의 속력은 낙하거리에 비례한다고 가정하고서 그것이 모순을 내포하기 때문에, 척도를 낙하거리로부터 낙하시간으로 바꾸어 고찰해 왔는데, 이것이 반드시 유일한 방법인 것만은 아니었다는 것을 알았다. 즉 속력이 낙하거리에 비례할 경우는 불가능하더라도 낙하거리의 제곱에 비례할 경우, 제곱근에 비례할 경우 등을 차례로 검토해 나가면, 제곱 쪽은 역시 모순을 내포하고 있어도, 제곱근 쪽은 모순 없이 마찬가지로 올바른 결론에 다다를 수 있을 것이다.
스트레스가 계속되면 신체는 어떻게 변할까?
Home - SCIENCE WAVE사이언스 웨이브(Science Wave)는 세상을 과학의 눈으로 바라봅니다. 최신 과학뉴스와 누구나 쉽고 재미있게 볼 수 있는 과학상식을 전달합니다.sciencewave.kr 인간이 태어나 사회에
sciencewave.tistory.com
'과학 상식' 카테고리의 다른 글
| 따개비와 홍합이 물속에서 초강력 접착제를 만드는 이유 (0) | 2025.02.13 |
|---|---|
| 목성 대적점에서 제임스웹이 발견한 새로운 현상 (1) | 2025.02.13 |
| 스트레스가 계속되면 신체는 어떻게 변할까? (0) | 2025.02.13 |
| 셀로판테이프의 끈끈함은 어떻게 유지될까? (0) | 2025.02.13 |
| 대기층과 대기의 성분 (0) | 2025.02.13 |